Capacitors are passive electronic components that provide energy storage in the form of an electrostatic field. A capacitor charges up when the AC reaches its peak in an AC circuit and releases the charge when the AC decreases. This behavior allows the capacitor to act like temporary storage that causes the current to lead voltage by 90 degrees.
Electrical engineers use capacitors to improve the power factor in an AC circuit. For example, an AC circuit powering inductive loads like a motor results in a lagging current. Adding a capacitor helps compensate for the lagging current and brings the power factor closer to unity. Power factor correction improves the efficiency of energy usage and reduces electricity bills.
In PCB design, capacitors are often used in low pass or high pass filters. This is because the capacitor's impedance is a factor of the AC signal frequency that passes through it. A capacitor typically blocks lower frequency signals while allowing higher frequency signals to pass through.
The capacitor is shunted to the ground. As such, high frequency signals are channeled to the ground. This prevents high frequency noise above the cut-off frequency from passing through to the load.
A low pass RC filter's cutoff frequency is defined by the following equation.
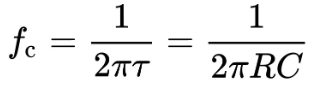
You can understand the filter's behavior better by its transfer function with the following Laplace transform.
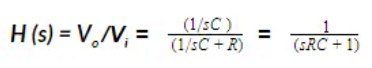
Meanwhile, the capacitor is connected in series with the incoming signal to form a high pass filter. Based on the below diagram, the capacitor blocks DC or low-frequency signals from passing through to the load. Only signals above the cut-off frequency are allowed to pass.
The cutoff frequency of the RC high pass filter is as follows:
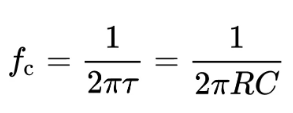
The high pass RC filter's transfer function is given by the following equation.
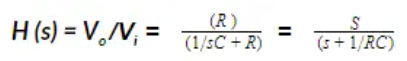
A capacitor incorporates two conductive plates separated by an insulating material called the dielectric. A capacitor's capacitance is directly proportional to its plate's surface area and inversely proportional to the plate's separation. Capacitance is also dependent on the dielectric constant of the substance separating these plates.
Capacitance is expressed by the following equation:
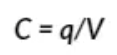
Where C is capacitance, q is the electrical charge, and V is the differential potential across conductive plates.
Previous: Turnbuckles Selection Guide
Next: Global Optical Module Market: Towards High Speed 400G Optical Modules
Copyright:@2020-2021
Comments Please sign in or sign up to post.
0
0 of 500 characters used